Неочевидные закономерности

Тысячи игроков пытались и будут пытаться открыть секрет рулетки, найти правило выпадения цифр и использовать его для обеспечения выигрыша. Мы рассмотрели три примера, в которых на протяжении 19 спинов этот «секрет» был очевиден.

Рассмотрим теперь первую последовательность из приведенных выше:

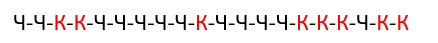
Найдете ли вы в ней закономерность, используя которую можно выиграть 19 раз подряд?..

Чтобы увидеть ее, надо хотя бы на короткое время забыть о том, что колесо рулетки не имеет памяти, и предыдущие результаты никак не влияют на последующие.

Альтернативные равновероятные события обозначим как 1 и -1. Будем записывать последовательность результатов и договоримся, что:

• последовательное выпадение двух разноименных результатов = событие 1;
• последовательное выпадение двух одноименных результатов = событие -1;
• результат, полученный таким образом, запишем в таблицу справа внизу от исходных;
• последовательность, сформированную по вышеописанному алгоритму, назовем зависимой.

Получили четыре возможных комбинации и два определяемые ими события.

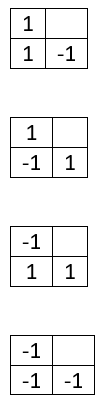
Вероятности четырех исходных комбинаций одинаковы и равны ¼, поэтому вероятности событий 1 или -1 в зависимой цепи тоже одинаковы и равны ½.

Получается, с каждым новым спином в зависимой последовательности добавляется запись о новом событии. Например,

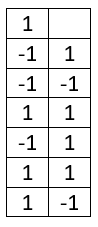
Исходные результаты случайны и равновероятны – это ведь рулетка. Таким образом, в зависимой последовательности результаты каждого спина тоже случайны и равновероятны.

Можно представить себе двух наблюдателей: первый сидит за настоящим столом, видит крупье, колесо и шарик и по телефону диктует результаты второму наблюдателю. Но сообщает не реальное событие, а событие, рассчитанное по вышеописанному алгоритму. Второй наблюдатель тоже ведет запись и записывает то, что слышит.

В итоге у нас имеются записи о двух разных (!) равновероятных случайных процессах, обусловленных вращением одного и того же колеса рулетки.

Начиная с третьего события в такой игре, можно вести запись второй зависимой последовательности, для которой исходной является первая зависимая цепь. И т.д. – вот исходная последовательность в полной записи.

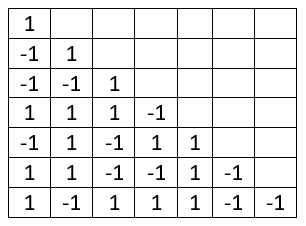
Обратите внимание, единственное событие в крайней правой цепи, зависит от каждого из предыдущих событий рулетки. Если изменить любое исходное и пересчитать таблицу, результат правой нижней ячейки изменится на противоположный.

Мы получили парадоксальный результат: если достаточно долго наблюдать за игрой и взять любую из зависимых последовательностей, она будет обладать следующими свойствами:

• это будет абсолютно случайная последовательность, потому что она получена на основании результатов рулетки – общепризнанного инструмента обеспечения случайного выбора. Для такого случайного процесса справедливо утверждение, что каждое событие не зависит от предыдущих;
• как мы только что показали, каждое событие этой последовательности зависит от событий, которые произошли ранее.

На рисунке - сверху вниз запись игры, где равновероятные исходы обозначены цифрами 1 и -1, а также цветом ячейки (1 – зеленый, -1 – красный), колонка №1 – результаты реальных спинов, колонки 2-46 – зависимые.

Спины 27-46 – это рассмотренная выше последовательность, для которой было предложено найти правило, обеспечивающее выигрыш 19-ти ставок подряд - Ч-Ч-К-К-Ч-Ч-Ч-Ч-Ч-К-Ч-Ч-Ч-Ч-К-К-К-Ч-К-К.

Как видим, оно простое: начиная со второго хода, ставь на тот же результат в 24-й зависимой последовательности. На каждом ходу легко рассчитать, какой результат должен выпасть в исходной цепи, чтобы в 24-ей зависимой на том же спине получилась единица. Конечно, при условии, что вам известны предыдущие результаты 1-26 спинов.

Получается, в одном и том же случайном процессе два наблюдателя видят ситуации с совершенно разными ожиданиями. Тот, кто наблюдает за рулеткой, не замечает ничего особенного – «обычная случайность». Наблюдатель за 24-й зависимой цепью видит «редкое» событие и с каждым ходом все больше ожидает, что в его последовательности сплошных единиц выпадет наконец-то -1. И на его ожидание влияет история случившихся ранее событий.

Глядя на зависимые цепи, мы можем следить за игрой глазами не одного, а многих наблюдателей. Это делает рулетку намного более увлекательной.