Что бывает, когда толпа всегда права и когда толпа всегда ошибается

Представление произвольно взятого прогноза равновероятной игры в виде некоего «голосования» растущей с каждым ходом толпы наблюдателей с разными ожиданиями интересно тем, что эта модель позволяет создавать гипотезы для прогнозирования на небольших промежутках игры. Стоит поразмышлять.

Как говорил Эдгар По, «мнение большинства — всегда ошибочно, ибо большинство людей — идиоты». Гальтон утверждал, что большинство людей «тупы и невежественны», но суммарный прогноз толпы верный.

Кому верить? Понятно, что наши зависимые наблюдатели не люди, а всего лишь числа. Но немного антропоморфизма не повредит. Это вряд ли больший грех, чем видеть в графиках котировок «голову и плечи», «трех черных ворон», «вымпелы», «бабочек» с «крабами», «флаги», «бриллианты», «летучих мышей» и др. паттерны классического теханализа.

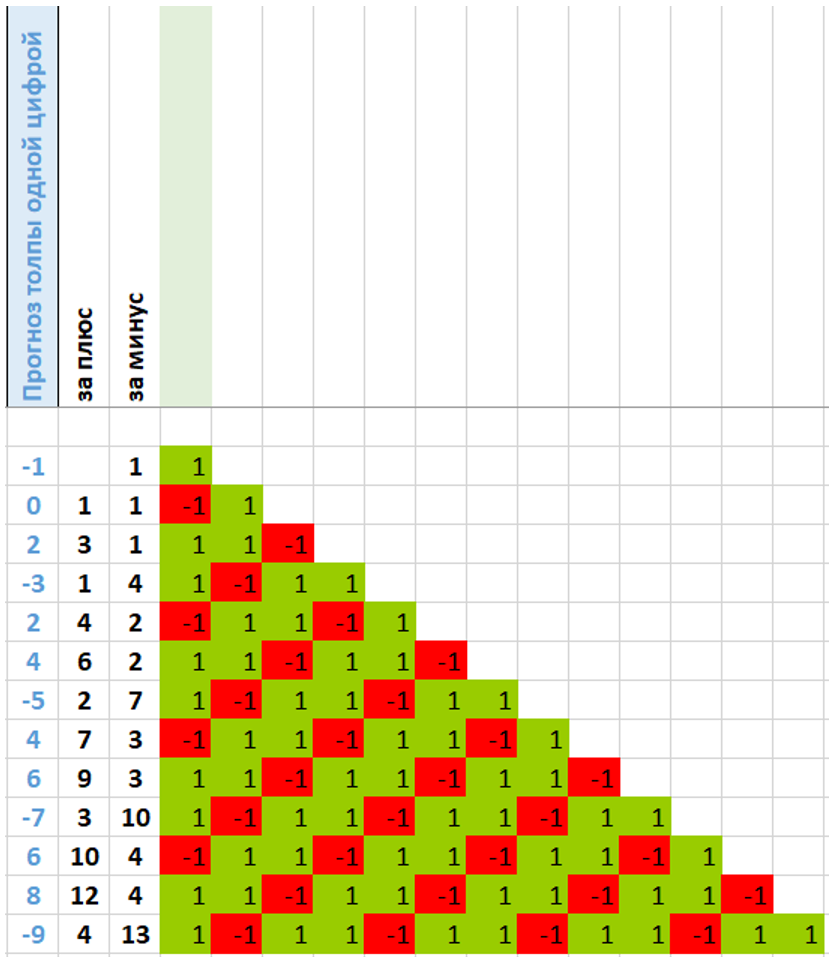
Можно ли утверждать, что толпа всегда права? См. рисунок – это зависимые цепи, сформированные при условии, что прогноз толпы всегда верен. Как видим:

• случайности нет;
• сумма результатов +1 и -1 в массиве не стремится к нулю, хотя должна, если игру считать равновероятной. Она стремится к 2:1 в пользу плюса.

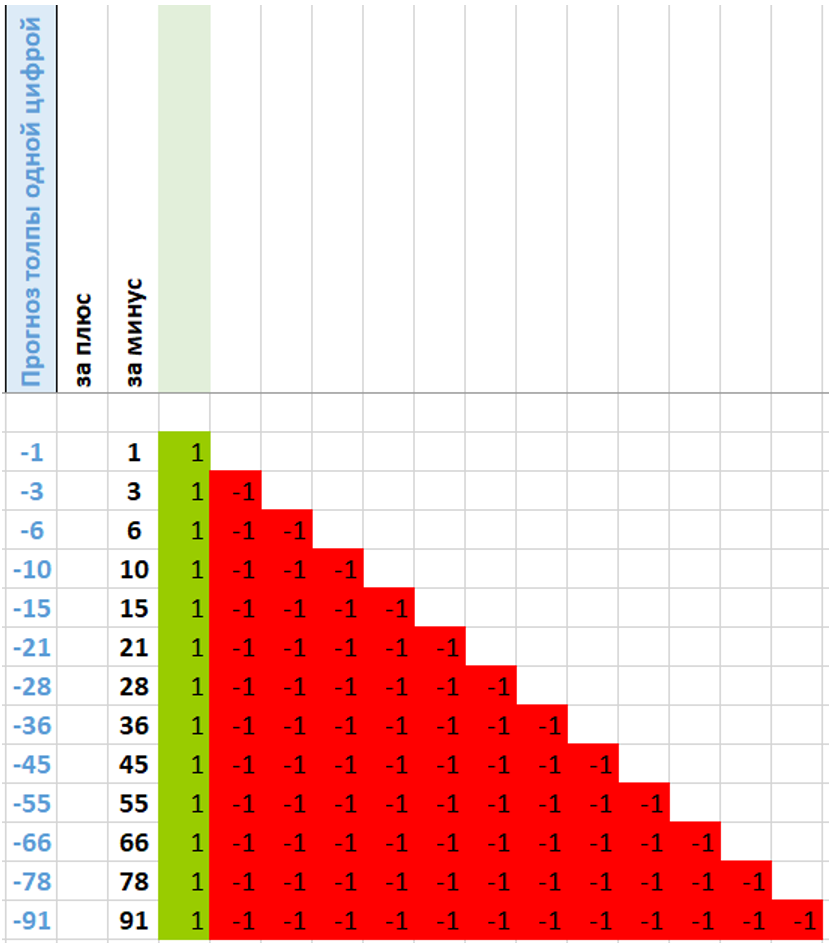
Т.е. толпа - не всегда права. Взглянем на обратную задачу, пусть толпа всегда ошибается. Смотрим:

• случайность снова исчезла;
• сумма результатов всех цепей стремится к минус бесконечности, что тоже не соответствует условию равновероятности.

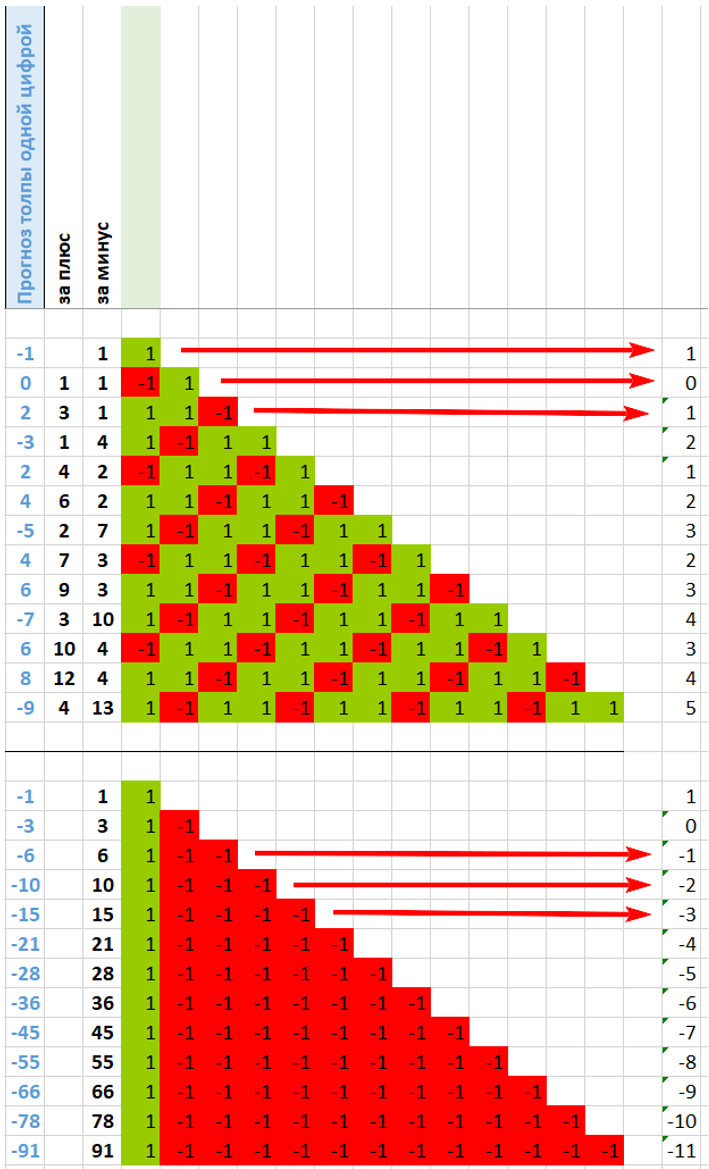
Отметим, что в случаях, когда толпа права, сумма событий в строке положительна; когда толпа ошибается – отрицательна.

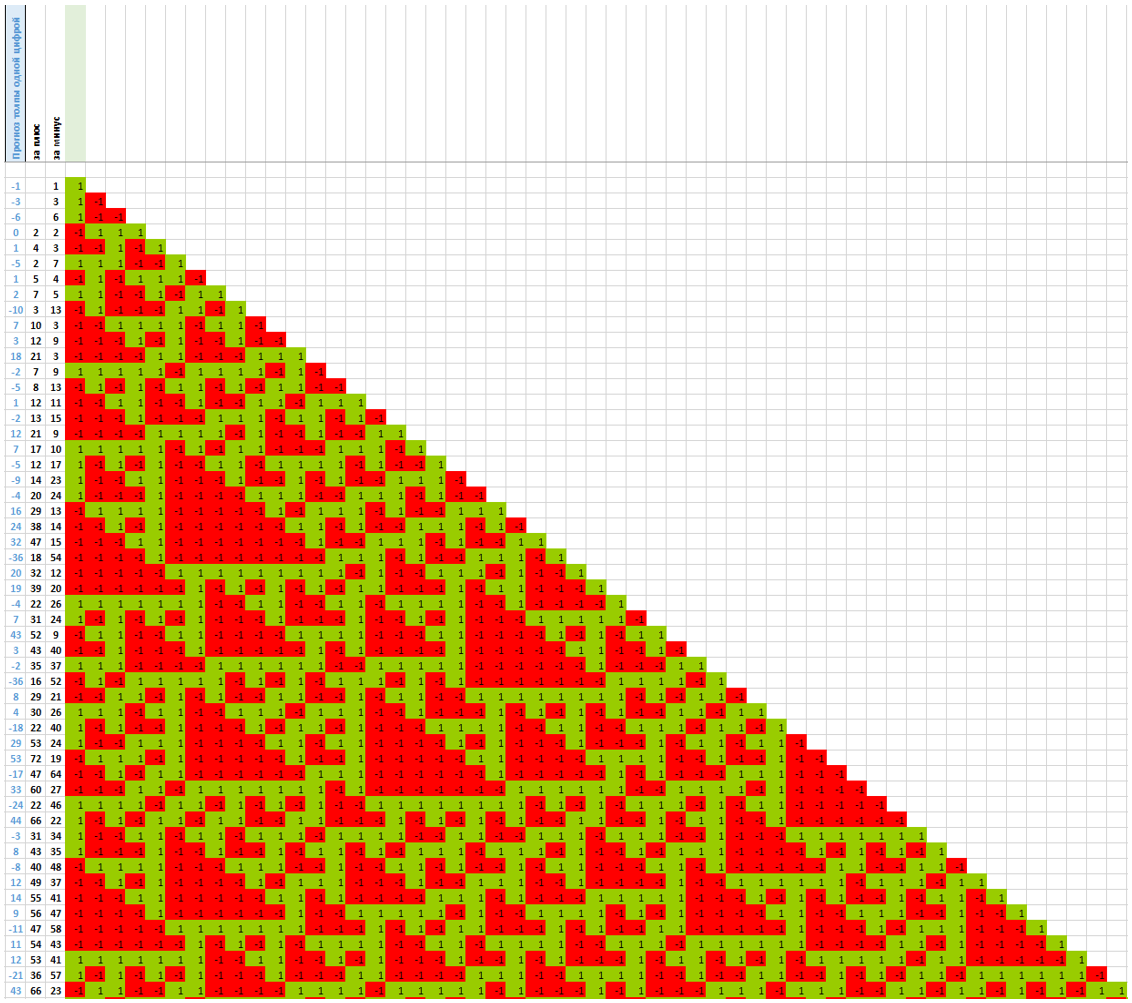
Получается, толпа иногда права, а иногда нет. В реальном случайном процессе зависимые цепи выглядят примерно так.