Как оценить равновесие

Как показано выше, попытка опереться на «мудрость толпы» уничтожает случайность; последовательность, в которой каждый шаг определяется торжеством демократии, является детерминированной. При этом сумма альтернативных результатов +1 и -1 во всех цепях стремится совсем не к нулю, как было бы положено для случайного равновероятного процесса.

Рассмотрим эту сумму. Каждый наблюдатель на каждом ходе видит событие 1 или -1. Каждый ход добавляется один новый наблюдатель. На каждом ходе одномоментно фиксируется количество новых событий равное номеру хода. События можно складывать, обнуляя парные 1 и -1. На рисунке ниже показана ситуация, когда за 22 хода (реальная случайная цепь) наблюдатели «увидели» 253 события, и сумма этих событий равна 1.

Колонка таблицы («Сумма событий в строке при следующем = 1») показывает расчет, какое число будет добавлено к общей сумме массива в том случае, если следующее событие исходной цепи будет равно единице. Обратите внимание, если на очередном ходе в исходной цепи действительно выпадает единица, то сумма равна расчетному значению: на третьем ходе (3), на пятом (1), на седьмом (-1), на десятом (4) и т.д. Если же выпала минус единица, то расчет даст то же значение, но с обратным знаком: на шестом ходе (-2), на восьмом (-4), на девятом (3) и т.п.

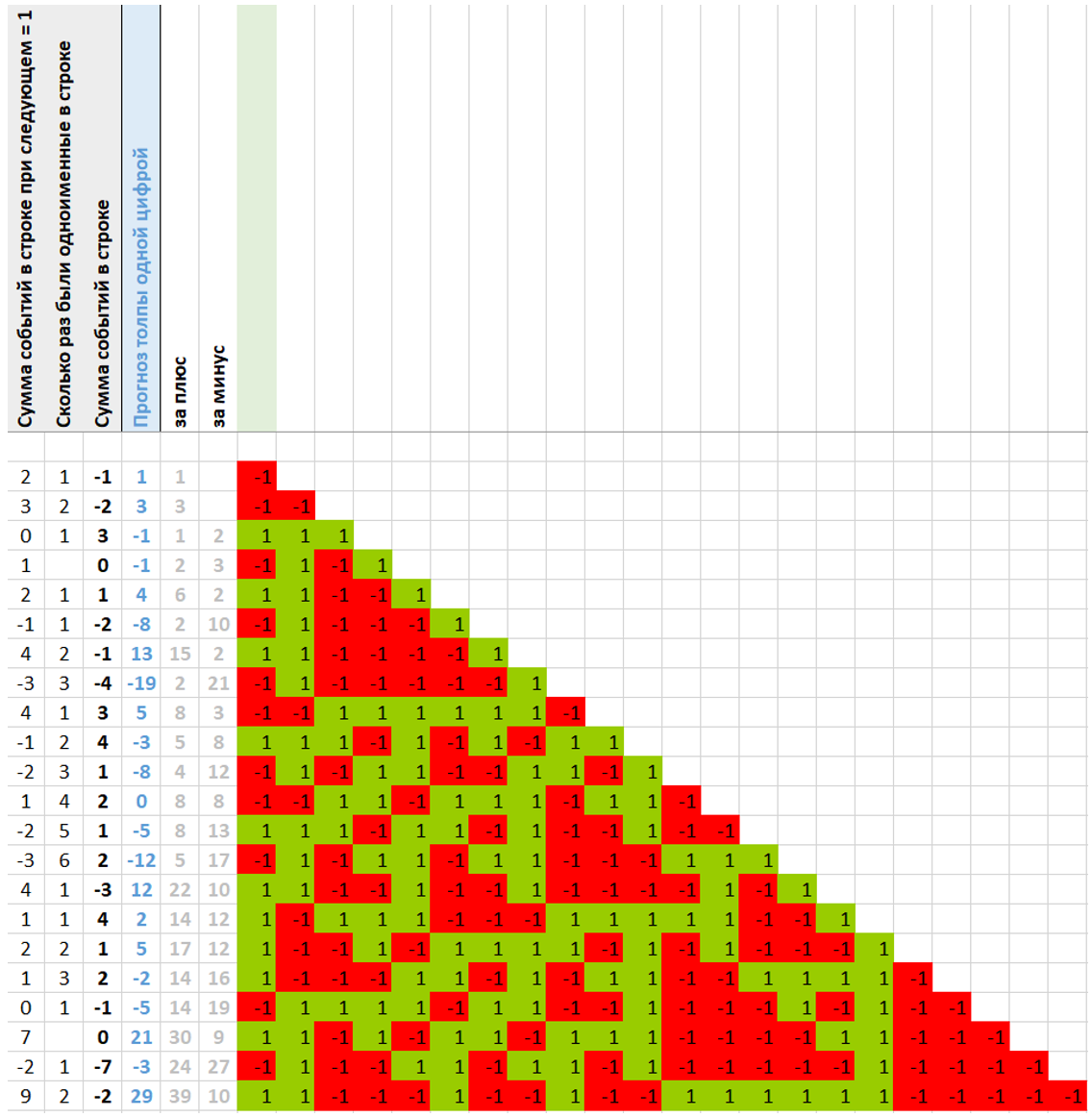
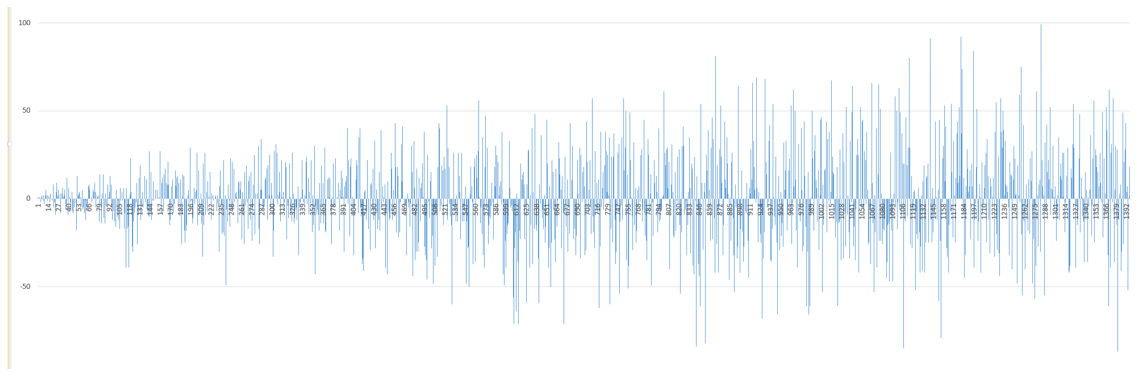
Получается, Фортуна поддерживает некое равновесие и с каждым новым ходом добавляет к сумме массива наблюдаемых событий то положительное, то отрицательное число так, чтобы нарастающая сумма была примерно равна нулю – именно этого мы и ждем от случайной равновероятной игры. Вот диаграмма этого показателя на большой (1400+ ходов) игре. Чередование очевидное – то плюс, то минус.

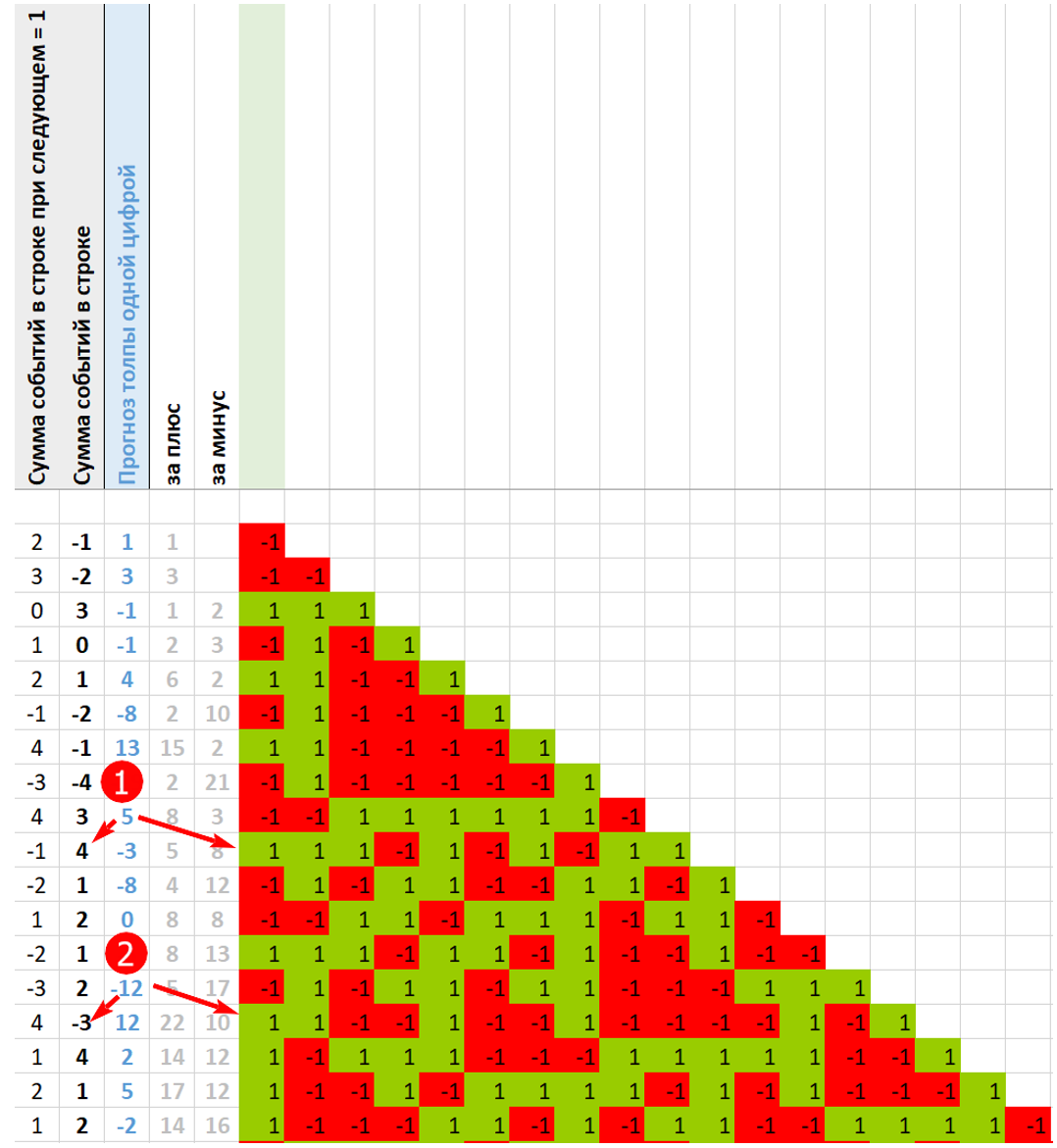
Хорошо видно, если на очередном ходе к общей сумме добавляется положительное слагаемое, значит, ожидание «толпы» наблюдателей было верным (1 на рис. ниже). Если отрицательное – толпа ошиблась (2 там же).

Получается, если мы видим, что на протяжении N ходов в массив добавлялись только положительные суммы, то это ситуация «толпа была права, а она не может быть всегда права, т.е. сейчас-сейчас ошибется», и на N+1 ходу можно ожидать появления суммы отрицательной. И наоборот. Легко рассчитать, какое событие должно выпасть в исходной цепи, чтобы такое ожидание сбылось. Чем больше N (отклонение от равновесия), тем ожидание сильнее.

Упростим запись (см. рис. ниже). Показана ситуация, когда на протяжении трех ходов в массив добавлялись отрицательные суммы. Чтобы исправить это «отклонение» ожидается, что прогноз толпы все же окажется верным.

Если в прогнозах ориентироваться только на добавляемую в массив сумму (добавилось плюсов – пусть теперь добавится минусов, и наоборот), то количество противоположных событий в массиве выравнивается, но и эта картина совершенно не похожа на «случайную».

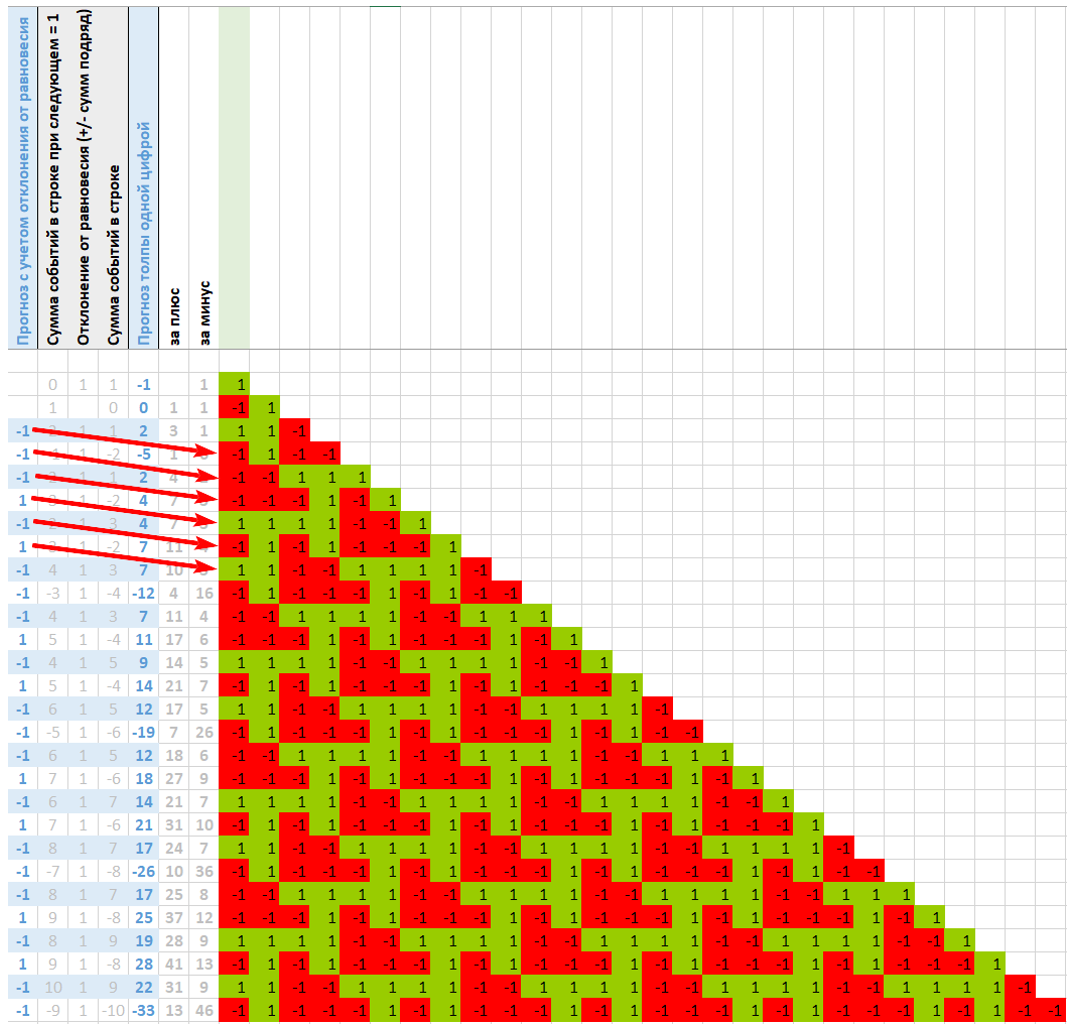
На каждом втором шаге прогнозы толпы и суммы противоположны, и нет подходящей идеи выбора того или иного варианта.

Регулируя сумму событий в строке, Фортуна умудряется решать все задачи: поддерживать баланс противоположных событий на равновесном уровне и обеспечивать «случайность» каждой наблюдаемой последовательности. Когда в массиве становится слишком много отрицательных событий (-1), начинают сбываться прогнозы толпы, и ситуация выравнивается. Наоборот, слишком много положительных событий ведет к тому, что прогнозы толпы начинают НЕ сбываться. Сколько считать за «слишком много», к сожалению, точно не определяется.

Сумма событий далеко не единственный показатель, который можно использовать подобным образом.

   Пред.       |       След.