Максимумы

Ранее была показана ситуация, когда два наблюдателя совершенно по-разному видят один и тот же случайный процесс. Последние двадцать шагов в сравнении выглядят так:

Назовем максимумом последовательность следующих подряд одинаковых событий, для которой в рассматриваемый момент времени нет большей или равной ни в исходной, ни в зависимых случайных цепях. Определение не особо изящное, но как уж есть. Вот пояснения.

Здесь нет максимума, есть три одинаковых самых больших последовательности.

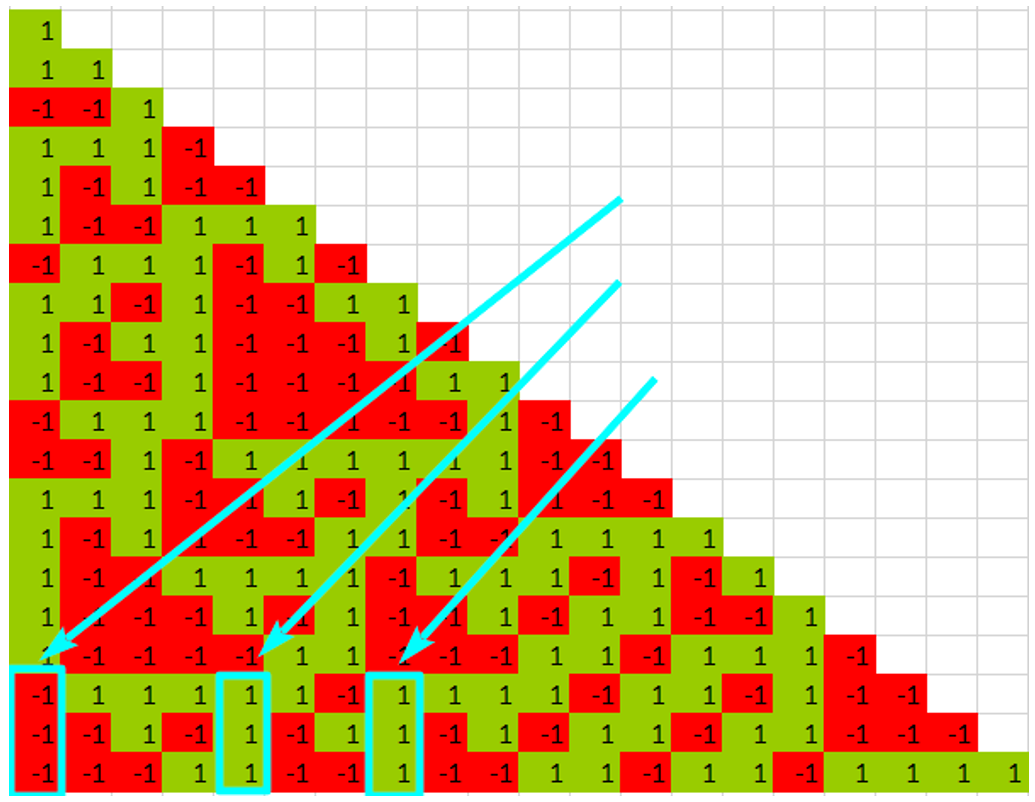
А здесь максимум есть – последовательность из четырех единиц подряд на данный момент самая большая во всех зависимых цепях, включая исходную.

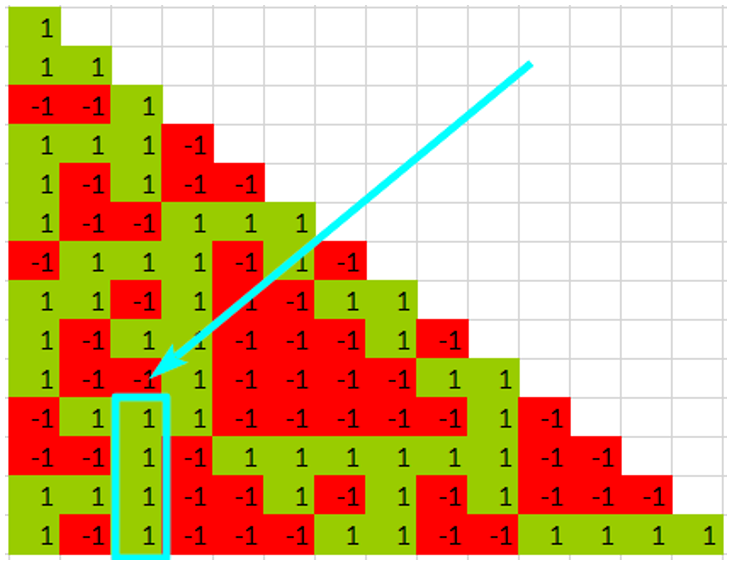
Поиск и подсчет максимумов позволяет представить картину ожиданий еще лучше. Очевидно, любой максимум рано или поздно «закроется» - в его цепи произойдет не одноименное, а альтернативное событие. Какое событие должно случиться в исходной цепи – рассчитать легко. Например, на рисунке.

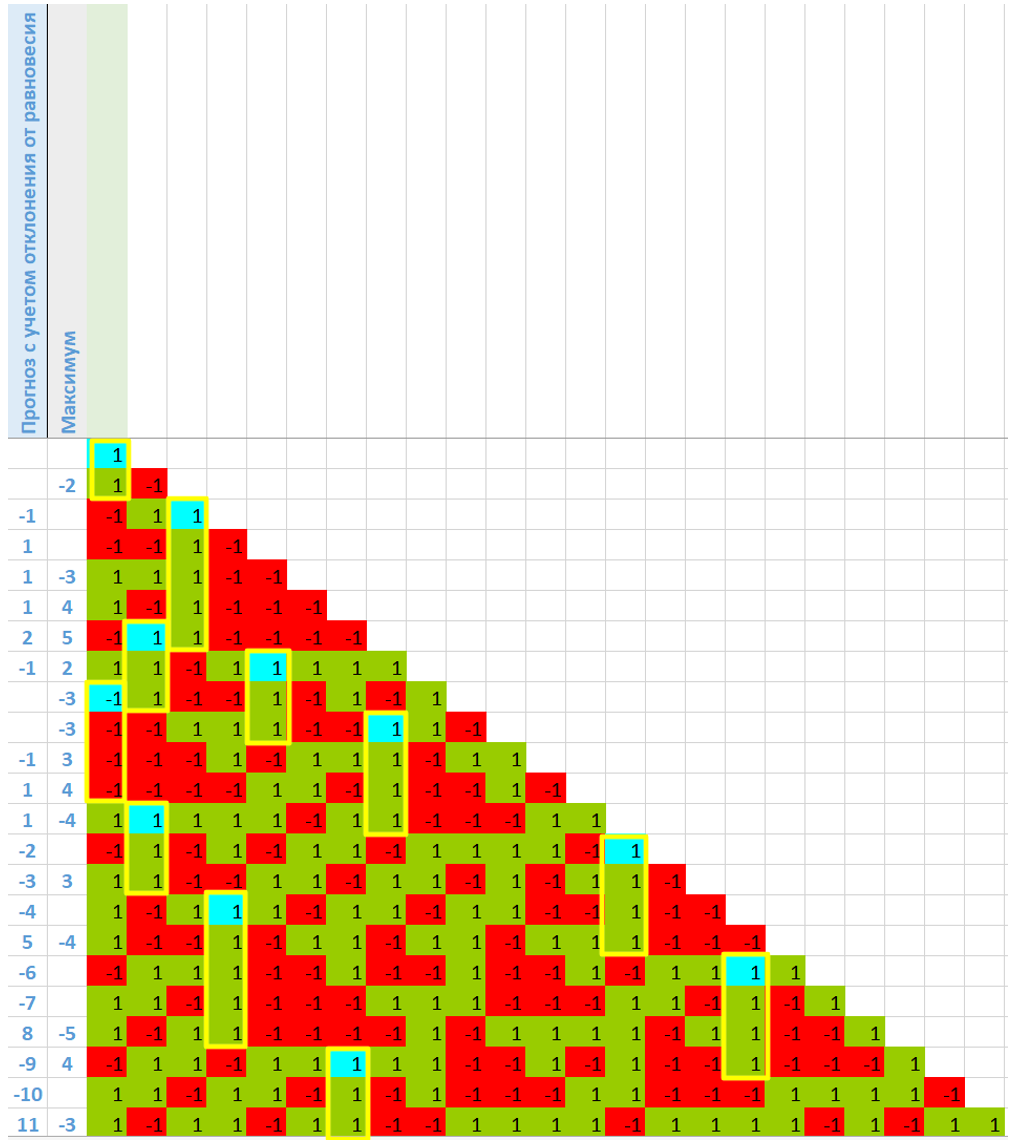
Видно, что в половине случаев прогнозы, основанные на ожидании положительной или отрицательной суммы строки противоположны прогнозам, основанным на ожидании «закрытия» максимума.

Но и это еще не все! :0)

На рисунке ниже показано, как тот же принцип ожидания закрытия максимума использован для последовательностей одноименных событий, расположенных по диагонали. И у нас уже три (!) прогноза - какое событие должно произойти в реальной цепи, чтобы закрылся диагональный максимум, тоже легко рассчитывается.

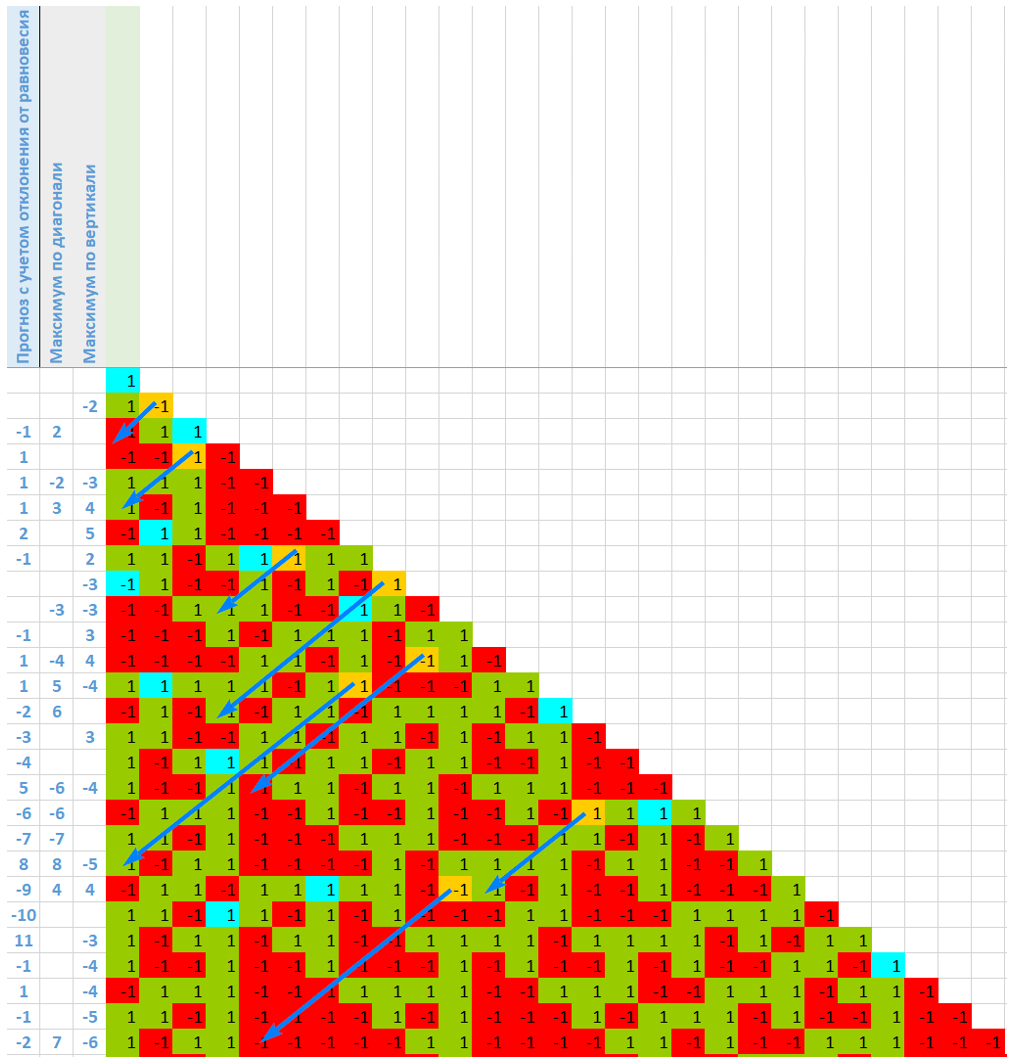
И все эти прогнозы обязательно сбудутся в самом ближайшем будущем.

   Пред.       |       След.