Удвоенная прибыль при нулевом риске (ставка вне времени)

Чем интересно такое представление биржевых данных.

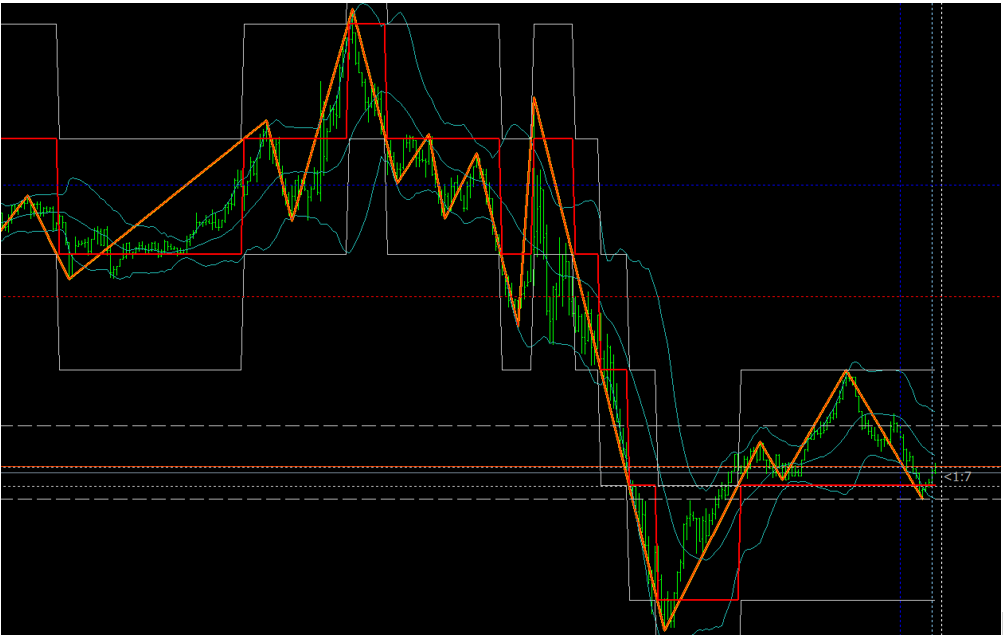
См. рис. ниже - это результаты расчетов по описанной ранее методике для последовательности событий 1 или -1, последний этап которой показан на рис. выше. Длина расчетной последовательности 450 событий (16500+ баров графика).

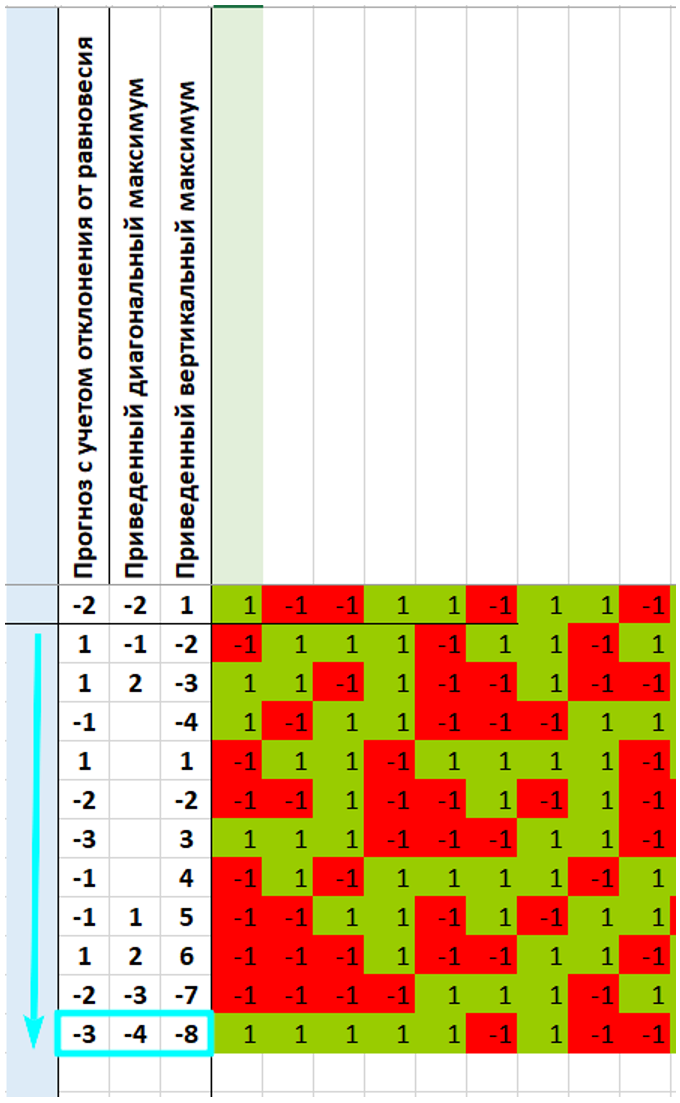
Прогноз суммы = -3, т.е. в третий раз сумма событий строки одинаковая, и ожидается событие -1, чтобы эта полоса закончилась. Для вертикального и диагонального максимумов тоже ожидается событие -1. Масштаб иллюстраций мелкий, потому что рассчитанная последовательность длинная.

Вертикальный максимум последовательности.

Диагональный максимум последовательности.

К тому же, это уже третий прогноз, когда ожидания по всем трем параметрам совпадают, и первые два не сбылись (сыщик Урдорф радостно потирает руки). Ожидание очевидно: -1.

Здесь начинается различие между казино и биржей. Если бы мы при аналогичном расчете делали ставку, например, на красное/черное, то при сбывшемся прогнозе получили бы выигрыш в размере ставки, а при несбывшемся крупье забрал бы нашу ставку себе. Вероятность исходов 1 к 1, риск 1 к 1, и выигрыш/проигрыш тоже 1 к 1. Ставки делаются заранее, после запуска шарика новые ставки не принимаются, поэтому отношение риска к прибыли всегда одинаковое.

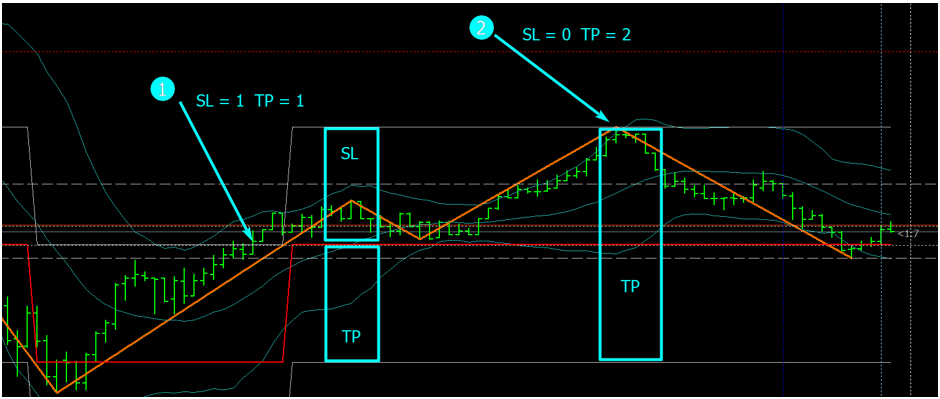
Далее на рис. показана точка (1), в которой было зафиксировано последнее событие на графике, соответственно, сразу же был сделан расчет ожиданий: -3 | -4 | -8. Если открыть короткую позицию в этой точке, и линия ЗигЗага пересечет уровень +N пунктов (серая горизонтальная линия сверху), произойдет очередное событие последовательности равное 1, и мы зафиксируем убыток в N пунктов по стоп-лоссу. Если линия ЗигЗага пойдет вниз и пересечет уровень –N пунктов (серая горизонтальная линия снизу), мы получим прибыль в N пунктов по тейк-профиту. В точке 1 и TP и SL равны N пунктам, соответственно, риск сделки 1 к 1.

Этот расчет не изменится до тех пор, пока не произойдет очередное событие, как бы ни колебалась ломаная ЗигЗага между уровнями, при достижении любого из которых будет считаться, что новое событие произошло. Но в точке (2) рассчитанное в точке (1) ожидание все то же, а соотношение TP к SL равно 2 к 0. Как видно на графике, кривая коснулась уровня, но не пересекла его и развернулась, новое событие не было зафиксировано. Таким образом, открывая позицию в точке (2), мы имели возможность получить прибыль в 2N пунктов при практически нулевом риске.

Если принять гипотезу о равной вероятности событий 1 и -1, получается, на бирже у нас есть возможность открыть позицию при более выгодном соотношении риска к прибыли.

Можно ли было воспользоваться ей? Почему бы нет?

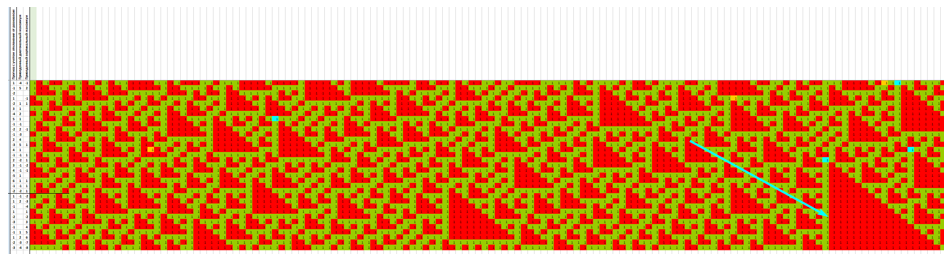
Ситуации, в которых соотношение TP/SL в нашей модели изменяется в пользу игрока (читай – трейдера), случаются очень часто, практически между каждыми двумя событиями. На рис. ниже голубыми прямоугольниками отмечены интервалы, когда соотношение TP/SL для текущей равновероятной пары событий было в пользу трейдера. Приемлемый для себя риск трейдер может выбрать самостоятельно.

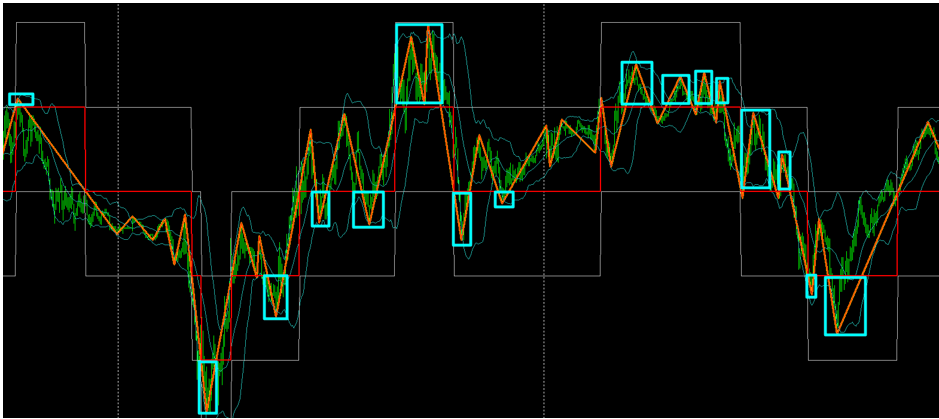
Это немного необычное представление об игре. Привычный ход действий: выбор ожидаемого события => ставка => выигрыш/проигрыш и далее по тому же циклу. В нашем случае между выбором ожидаемого события (он делается на основании изучения истории игры - собственно это и является предметом технического анализа) и ставкой проходит некоторое время, в течение которого отношение риска к прибыли изменяется, а расчетное ожидание остается прежним. Трейдер словно оказывается «вне времени» случайной игры и получает возможность делать ставки на равновероятные события с неравными отношениями риска и прибыли.

В настоящей равновероятной игре такая возможность ведет к статистическому выигрышу. Представьте, что вы будете в орлянке терять один рубль при проигрыше, а за выигрыш получать три рубля – возврат ставки плюс два рубля сверху. А на бирже?..

«Теория» выглядит заманчиво. Практика, увы, сложнее, но - интереснее.

   Пред.       |       След.